大学受験に限らず高校受験や中学受験の際にも“偏差値”というワードを耳にします!
“偏差値”と言うワードを聞いてみなさんが思い浮かぶのは、
偏差値が高いと頭のいい学校なんだなぁ〜
偏差値50って真ん中かぁ〜
と言う感じでしょう。
そこで!!!
今回は、受験の目印となる偏差値について単純に表面的な意味だけではなく、“偏差値とは何か”を数学の統計学的な観点から簡単にですが紹介していきます!
学歴厨の方。この記事を読んでニヤニヤしてください(笑)。
文系の方。読んだら頭が痛くなりますよ(笑)。
そして理系の方。この記事の下の方では数式やグラフを使って偏差値を紹介しているのでよろしければ数学1Aの「データの分析」の内容の一環としてご覧ください!!
偏差値と学力の関係性

偏差値とは。。。
こちらはコトバンクより引用したものです。まずは読んでみてください。
偏差値とは個人の知能や学力や性格などについての検査結果が、集団の平均値よりもどれくらい上または下に偏っているかを、標準偏差を目盛りとして表すものである。
つまり、平均点を真ん中として自分がそこからどれだけ離れているのかを表すものになります。
大学を例に出すと、偏差値50を真ん中とした時にそれぞれの大学が平均からどれだけ上または下に位置しているのかを示すものです。
また、偏差値は以下の式を用いることによって求めることができます。
※ここでは数式の紹介のみですので、この式がどういう意味なのか。について興味がある方は下の偏差値の計算式の紹介をご覧ください
偏差値=(得点-平均点)÷標準偏差×10+50
偏差値50→55と55→60の違い

上で紹介したように、偏差値は基準からどれだけ上または下に偏っているかを示すものです。
ここで注意が必要なのが、偏差値50→55と55→60は全く別ということです。そして、これこそが偏差値を用いる理由なのです。
どう言うことか。。。
ここでは、数式は使わずに直感的に理解できるように例を通して紹介しようと思います。
単純に基準からの差が知りたければ一位から最下位までをランキングしてあげれば済みます。
しかし、1000人が受けたテストで平均点が500位の人の点数としたときに、500位から400位に上がるのと150位から50位に順位を上げるのは同じと言えるでしょうか?
同じではないですよね。直感的にも後者の方が難しいと感じるはずです。
つまり、ランキングだけで判断していてはその順位がどれだけ凄いのか。が変わらないのです。
そこで偏差値の登場です。偏差値では下の表1-1のようにどの偏差値に何%がいるのかがわかります。偏差値の差としては同じ5なのですが、より高い偏差値をとる方が難易度が上がるということです。

さて、
ここからは偏差値を数式やグラフからもみたい。という理系の物好きさんのために紹介していきます!興味のある方は読み進めてみたら面白いのではないでしょうか・・・
偏差値と正規分布の関係
正規分布とは??

偏差値の計算をするには正規分布について少し紹介する必要があります。
正規分布とは簡単に言うと以下の性質を持つ確率分布(現象の起こる確率を曲線で表したもの)のことです。
- 正規分布の形は平均と標準偏差(データのバラツキ)で決まる。
- 標準偏差がわかれば、その範囲にどれくらいの観測データが含まれているかが分かる
というものです。
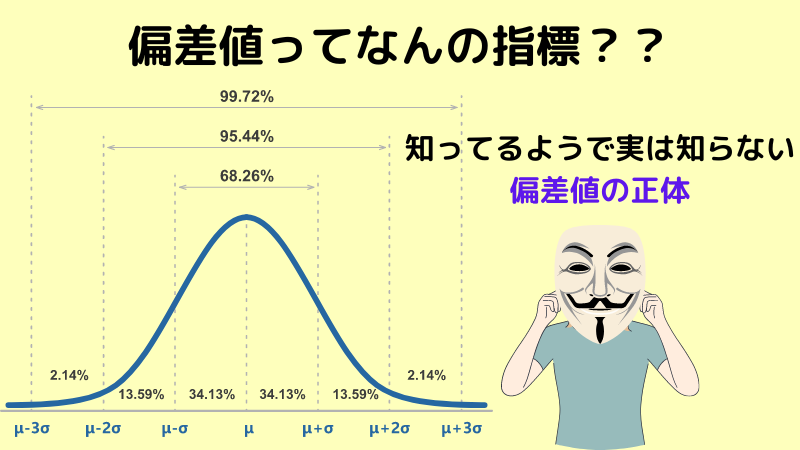
偏差値を例に出すと、偏差値は平均が50 ,標準偏差10 とした正規分布( 統計学ではN(50,10^2)と表します )に従います。
以下のグラフ1-1は偏差値の正規分布を示しています。

ではこのグラフの見方について簡単に説明すると、
データが正規分布に従うという前提のもとでは、標準偏差には下記のようなルールがあります。
- 平均値から±標準偏差1個分に含まれるデータは全体の約68%を占める
- 平均値から±標準偏差2個分に含まれるデータは全体の約95%を占める
下のグラフの矢印のように、赤い矢印は標準偏差(平均からのばらつき)が10であるため、偏差値40~60の間に全受験生の68%が属しているということになります。
緑の矢印は偏差値30~70。つまり標準偏差2個分であるため、全受験生の95%が属しているということがわかります。

正規分布かどうかを判断する方法
補足として、今回は“データが正規分布に従うという前提の下”としていますが、何を根拠にそう言えるのでしょうか。
データが正規分布に従うかどうかを確認する方法は、大きく分けて2つあります。
1, 度数分布図(ヒストグラム)や正規確率グラフを用いて視覚的に確認するか
2, 統計的手法を用いて客観的な評価をおこなうかである。
偏差値の場合、模試や学力調査テストを行った際の偏差値のヒストグラムが正規分布に似ているということから偏差値は正規分布に従うということがわかります。
また、正規分布は世の中の多くの現象に対して適用することができると言われています。
ex)身長。体重。雨粒の大きさ。
偏差値と正規分布の関係

さて、いよいよ偏差値と正規分布の関係について紹介していきます。
偏差値60(グラフ1-2の紫線)の受験生が全体でどの程度の割合に位置しているのか。
紫の線と青の正規分布が交わっている点は縦軸から0.025とわかりますので、偏差値60の人の割合は1000人中25人いるということがわかります。
また、偏差値60が上位何%かを知りたければ紫線から右側と正規分布と横軸とで囲まれる面積を求めてあげればわかります。
なぜ面積なのか。の理由は簡単で、偏差値60以上の人を全て足し合わせてあげれば偏差値60の人の全体の中での順位がわかるからです。そして今、偏差値は連続的な値を取るためシグマで足し合わせるのではなく積分によって面積を求めてあげればいいということになります。

学校のテストを以下の式にテストの平均と標準偏差を代入して計算すると正確な数値が出てきます。ので好奇心の旺盛な方はやってみるといいでしょう。学年全員のデータから標準偏差を出すのは大変だと思いますが。。。(笑)
偏差値を求めて自分で正規分布の値を求めるのは高校生には難易度が高いと思いますのでここでは割愛しますが、簡単に手順だけを紹介しておくと以下の手順で自分の偏差値が上位何%なのかを求めることができます。
- 平均と標準偏差をもとに以下の式に代入して偏差値を求める
偏差値=(得点-平均点)÷標準偏差×10+50 - 求めた偏差値を使って正規分布を標準化する
偏差値をαと置くと、
α〜(50,10^2)→Z〜(0,1)となるようにZ=(X-μ)/σと置き換える
※Xは自分の偏差値。μは平均。σは標準偏差。 - Zの値を使って標準正規分布の表から値を求める。
ここではざっくりとした値の%だけ紹介しておきます。




コメント